skfolio#
skfolio is a Python library for portfolio optimization and risk management built on top of scikit-learn. It offers a unified interface and tools compatible with scikit-learn to build, fine-tune, cross-validate and stress-test portfolio models.
It is distributed under the open-source 3-Clause BSD license.
skfolio is backed by Skfolio Labs, which provides enterprise support and SLAs for institutions.
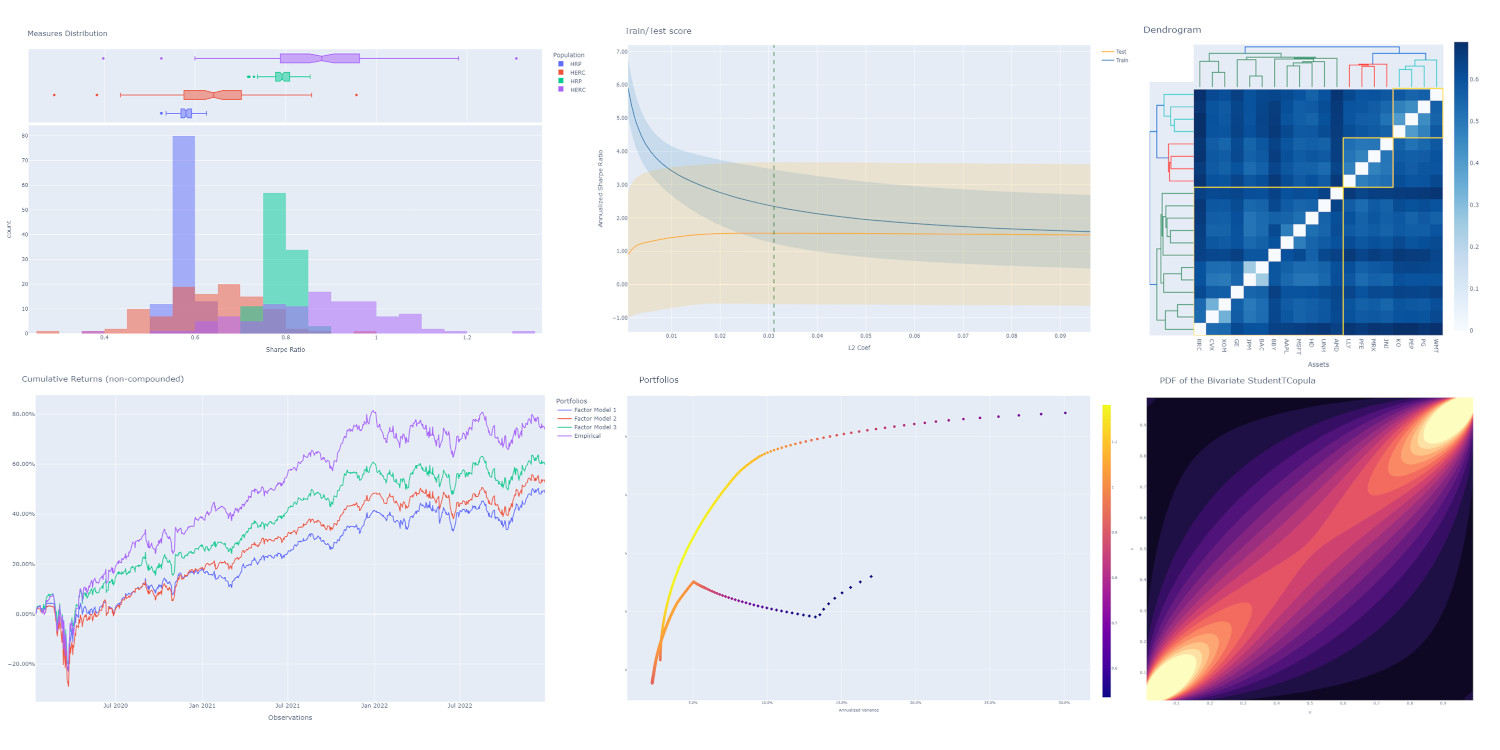
Important links#
Featured in#
Portfolio Optimization: Theory and Application by Daniel P. Palomar, includes Python code examples using skfolio.
Installation#
skfolio is available on PyPI and can be installed with:
$ pip install skfolio
Contribution#
We welcome contributions of all kinds. To get started, please visit our GitHub repository.
Whether it’s reporting a bug, suggesting an improvement, or submitting code, your input
helps make skfolio better.
Key Concepts#
Since the development of modern portfolio theory by Markowitz (1952), mean-variance optimization (MVO) has received considerable attention.
Unfortunately, it faces a number of shortcomings, including high sensitivity to the input parameters (expected returns and covariance), weight concentration, high turnover, and poor out-of-sample performance.
It is well-known that naive allocation (1/N, inverse-vol, etc.) tends to outperform MVO out-of-sample (DeMiguel, 2007).
Numerous approaches have been developed to alleviate these shortcomings (shrinkage, additional constraints, regularization, uncertainty set, higher moments, Bayesian approaches, coherent risk measures, left-tail risk optimization, distributionally robust optimization, factor model, risk-parity, hierarchical clustering, ensemble methods, pre-selection, etc.).
Given the large number of methods, and the fact that they can be combined, there is a need for a unified framework with a machine-learning approach to perform model selection, validation, and parameter tuning while mitigating the risk of data leakage and overfitting.
This framework is built on scikit-learn’s API.
Available models#
- Portfolio Optimization:
- Naive:
Equal-Weighted
Inverse-Volatility
Random (Dirichlet)
- Convex:
Mean-Risk
Risk Budgeting
Maximum Diversification
Distributionally Robust CVaR
Benchmark Tracker
- Clustering:
Hierarchical Risk Parity
Hierarchical Equal Risk Contribution
Schur Complementary Allocation
Nested Clusters Optimization
- Ensemble Methods:
Stacking Optimization
- Expected Returns Estimator:
Empirical
Exponentially Weighted
Equilibrium
Shrinkage
- Covariance Estimator:
Empirical
Gerber
Denoising
Detoning
Exponentially Weighted
Ledoit-Wolf
Oracle Approximating Shrinkage
Shrunk Covariance
Graphical Lasso CV
Implied Covariance
- Distance Estimator:
Pearson Distance
Kendall Distance
Spearman Distance
Covariance Distance (based on any of the above covariance estimators)
Distance Correlation
Variation of Information
- Distribution Estimator:
- Univariate:
Gaussian
Student’s t
Johnson Su
Normal Inverse Gaussian
- Bivariate Copula
Gaussian Copula
Student’s t Copula
Clayton Copula
Gumbel Copula
Joe Copula
Independent Copula
- Multivariate
Vine Copula (Regular, Centered, Clustered, Conditional Sampling)
- Prior Estimator:
Empirical
Black & Litterman
Factor Model
Synthetic Data (Stress Test, Factor Stress Test)
Entropy Pooling
Opinion Pooling
- Uncertainty Set Estimator:
- On Expected Returns:
Empirical
Circular Bootstrap
- On Covariance:
Empirical
Circular Bootstrap
- Pre-Selection Transformer:
Non-Dominated Selection
Select K Extremes (Best or Worst)
Drop Highly Correlated Assets
Select Non-Expiring Assets
Select Complete Assets (handle late inception, delisting, etc.)
Drop Zero Variance
- Cross-Validation and Model Selection:
Compatible with all
sklearnmethods (KFold, etc.)Walk Forward
Combinatorial Purged Cross-Validation
Multiple Randomized Cross-Validation
- Hyper-Parameter Tuning:
Compatible with all
sklearnmethods (GridSearchCV, RandomizedSearchCV)
- Risk Measures:
Variance
Semi-Variance
Mean Absolute Deviation
First Lower Partial Moment
CVaR (Conditional Value at Risk)
EVaR (Entropic Value at Risk)
Worst Realization
CDaR (Conditional Drawdown at Risk)
Maximum Drawdown
Average Drawdown
EDaR (Entropic Drawdown at Risk)
Ulcer Index
Gini Mean Difference
Value at Risk
Drawdown at Risk
Entropic Risk Measure
Fourth Central Moment
Fourth Lower Partial Moment
Skew
Kurtosis
- Optimization Features:
Minimize Risk
Maximize Returns
Maximize Utility
Maximize Ratio
Transaction Costs
Management Fees
L1 and L2 Regularization
Weight Constraints
Group Constraints
Budget Constraints
Tracking Error Constraints
Turnover Constraints
Cardinality and Group Cardinality Constraints
Threshold (Long and Short) Constraints
Quickstart#
The code snippets below are designed to introduce the functionality of skfolio so you
can start using it quickly. It follows the same API as scikit-learn.
For more detailed information see the Examples, User Guide and API Reference .
Imports#
from sklearn import set_config
from sklearn.model_selection import (
GridSearchCV,
KFold,
RandomizedSearchCV,
train_test_split,
)
from sklearn.pipeline import Pipeline
from scipy.stats import loguniform
from skfolio import RatioMeasure, RiskMeasure
from skfolio.datasets import load_factors_dataset, load_sp500_dataset
from skfolio.distribution import VineCopula
from skfolio.model_selection import (
CombinatorialPurgedCV,
WalkForward,
cross_val_predict,
)
from skfolio.moments import (
DenoiseCovariance,
DetoneCovariance,
EWMu,
GerberCovariance,
ShrunkMu,
)
from skfolio.optimization import (
MeanRisk,
HierarchicalRiskParity,
NestedClustersOptimization,
ObjectiveFunction,
RiskBudgeting,
)
from skfolio.pre_selection import SelectKExtremes
from skfolio.preprocessing import prices_to_returns
from skfolio.prior import (
BlackLitterman,
EmpiricalPrior,
EntropyPooling,
FactorModel,
OpinionPooling,
SyntheticData,
)
from skfolio.uncertainty_set import BootstrapMuUncertaintySet
Load Dataset#
prices = load_sp500_dataset()
Train/Test split#
X = prices_to_returns(prices)
X_train, X_test = train_test_split(X, test_size=0.33, shuffle=False)
Minimum Variance#
model = MeanRisk()
Fit on training set#
model.fit(X_train)
print(model.weights_)
Predict on test set#
portfolio = model.predict(X_test)
print(portfolio.annualized_sharpe_ratio)
print(portfolio.summary())
Maximum Sortino Ratio#
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
risk_measure=RiskMeasure.SEMI_VARIANCE,
)
Denoised Covariance & Shrunk Expected Returns#
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
prior_estimator=EmpiricalPrior(
mu_estimator=ShrunkMu(), covariance_estimator=DenoiseCovariance()
),
)
Uncertainty Set on Expected Returns#
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
mu_uncertainty_set_estimator=BootstrapMuUncertaintySet(),
)
Weight Constraints & Transaction Costs#
model = MeanRisk(
min_weights={"AAPL": 0.10, "JPM": 0.05},
max_weights=0.8,
transaction_costs={"AAPL": 0.0001, "RRC": 0.0002},
groups=[
["Equity"] * 3 + ["Fund"] * 5 + ["Bond"] * 12,
["US"] * 2 + ["Europe"] * 8 + ["Japan"] * 10,
],
linear_constraints=[
"Equity <= 0.5 * Bond",
"US >= 0.1",
"Europe >= 0.5 * Fund",
"Japan <= 1",
],
)
model.fit(X_train)
Risk Parity on CVaR#
model = RiskBudgeting(risk_measure=RiskMeasure.CVAR)
Risk Parity & Gerber Covariance#
model = RiskBudgeting(
prior_estimator=EmpiricalPrior(covariance_estimator=GerberCovariance())
)
Nested Cluster Optimization with Cross-Validation and Parallelization#
model = NestedClustersOptimization(
inner_estimator=MeanRisk(risk_measure=RiskMeasure.CVAR),
outer_estimator=RiskBudgeting(risk_measure=RiskMeasure.VARIANCE),
cv=KFold(),
n_jobs=-1,
)
Randomized Search of the L2 Norm#
randomized_search = RandomizedSearchCV(
estimator=MeanRisk(),
cv=WalkForward(train_size=252, test_size=60),
param_distributions={
"l2_coef": loguniform(1e-3, 1e-1),
},
)
randomized_search.fit(X_train)
best_model = randomized_search.best_estimator_
print(best_model.weights_)
Grid Search on embedded parameters#
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
risk_measure=RiskMeasure.VARIANCE,
prior_estimator=EmpiricalPrior(mu_estimator=EWMu(alpha=0.2)),
)
print(model.get_params(deep=True))
gs = GridSearchCV(
estimator=model,
cv=KFold(n_splits=5, shuffle=False),
n_jobs=-1,
param_grid={
"risk_measure": [
RiskMeasure.VARIANCE,
RiskMeasure.CVAR,
RiskMeasure.VARIANCE.CDAR,
],
"prior_estimator__mu_estimator__alpha": [0.05, 0.1, 0.2, 0.5],
},
)
gs.fit(X)
best_model = gs.best_estimator_
print(best_model.weights_)
Black & Litterman Model#
views = ["AAPL - BBY == 0.03 ", "CVX - KO == 0.04", "MSFT == 0.06 "]
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
prior_estimator=BlackLitterman(views=views),
)
Factor Model#
factor_prices = load_factors_dataset()
X, factors = prices_to_returns(prices, factor_prices)
X_train, X_test, factors_train, factors_test = train_test_split(
X, factors, test_size=0.33, shuffle=False
)
model = MeanRisk(prior_estimator=FactorModel())
model.fit(X_train, factors_train)
print(model.weights_)
portfolio = model.predict(X_test)
print(portfolio.calmar_ratio)
print(portfolio.summary())
Factor Model & Covariance Detoning#
model = MeanRisk(
prior_estimator=FactorModel(
factor_prior_estimator=EmpiricalPrior(covariance_estimator=DetoneCovariance())
)
)
Black & Litterman Factor Model#
factor_views = ["MTUM - QUAL == 0.03 ", "SIZE - TLT == 0.04", "VLUE == 0.06"]
model = MeanRisk(
objective_function=ObjectiveFunction.MAXIMIZE_RATIO,
prior_estimator=FactorModel(
factor_prior_estimator=BlackLitterman(views=factor_views),
),
)
Pre-Selection Pipeline#
set_config(transform_output="pandas")
model = Pipeline(
[
("pre_selection", SelectKExtremes(k=10, highest=True)),
("optimization", MeanRisk()),
]
)
model.fit(X_train)
portfolio = model.predict(X_test)
K-fold Cross-Validation#
model = MeanRisk()
mmp = cross_val_predict(model, X_test, cv=KFold(n_splits=5))
# mmp is the predicted MultiPeriodPortfolio object composed of 5 Portfolios (1 per testing fold)
mmp.plot_cumulative_returns()
print(mmp.summary()
Combinatorial Purged Cross-Validation#
model = MeanRisk()
cv = CombinatorialPurgedCV(n_folds=10, n_test_folds=2)
print(cv.summary(X_train))
population = cross_val_predict(model, X_train, cv=cv)
population.plot_distribution(
measure_list=[RatioMeasure.SHARPE_RATIO, RatioMeasure.SORTINO_RATIO]
)
population.plot_cumulative_returns()
print(population.summary())
Minimum CVaR Optimization on Synthetic Returns#
vine = VineCopula(log_transform=True, n_jobs=-1)
prior = SyntheticData(distribution_estimator=vine, n_samples=2000)
model = MeanRisk(risk_measure=RiskMeasure.CVAR, prior_estimator=prior)
model.fit(X)
print(model.weights_)
Stress Test#
vine = VineCopula(log_transform=True, central_assets=["BAC"], n_jobs=-1)
vine.fit(X)
X_stressed = vine.sample(n_samples=10_000, conditioning = {"BAC": -0.2})
ptf_stressed = model.predict(X_stressed)
Minimum CVaR Optimization on Synthetic Factors#
vine = VineCopula(central_assets=["QUAL"], log_transform=True, n_jobs=-1)
factor_prior = SyntheticData(
distribution_estimator=vine,
n_samples=10_000,
sample_args=dict(conditioning={"QUAL": -0.2}),
)
factor_model = FactorModel(factor_prior_estimator=factor_prior)
model = MeanRisk(risk_measure=RiskMeasure.CVAR, prior_estimator=factor_model)
model.fit(X, factors)
print(model.weights_)
Factor Stress Test#
factor_model.set_params(factor_prior_estimator__sample_args=dict(
conditioning={"QUAL": -0.5}
))
factor_model.fit(X, factors)
stressed_dist = factor_model.return_distribution_
stressed_ptf = model.predict(stressed_dist)
Entropy Pooling#
entropy_pooling = EntropyPooling(
mean_views=[
"JPM == -0.002",
"PG >= LLY",
"BAC >= prior(BAC) * 1.2",
],
cvar_views=[
"GE == 0.08",
],
)
entropy_pooling.fit(X)
print(entropy_pooling.relative_entropy_)
print(entropy_pooling.effective_number_of_scenarios_)
print(entropy_pooling.return_distribution_.sample_weight)
CVaR Hierarchical Risk Parity optimization on Entropy Pooling#
entropy_pooling = EntropyPooling(cvar_views=["GE == 0.08"])
model = HierarchicalRiskParity(
risk_measure=RiskMeasure.CVAR,
prior_estimator=entropy_pooling
)
model.fit(X)
print(model.weights_)
Stress Test with Entropy Pooling on Factor Synthetic Data#
# Regular Vine Copula and sampling of 100,000 synthetic factor returns
factor_synth = SyntheticData(
n_samples=100_000,
distribution_estimator=VineCopula(log_transform=True, n_jobs=-1, random_state=0)
)
# Entropy Pooling by imposing a CVaR-95% of 10% on the Quality factor
factor_entropy_pooling = EntropyPooling(
prior_estimator=factor_synth,
cvar_views=["QUAL == 0.10"],
)
factor_entropy_pooling.fit(X, factors)
# We retrieve the stressed distribution:
stressed_dist = factor_model.return_distribution_
# We stress-test our portfolio:
stressed_ptf = model.predict(stressed_dist)
Opinion Pooling#
# We consider two expert opinions, each generated via Entropy Pooling with
# user-defined views.
# We assign probabilities of 40% to Expert 1, 50% to Expert 2, and by default
# the remaining 10% is allocated to the prior distribution:
opinion_1 = EntropyPooling(cvar_views=["AMD == 0.10"])
opinion_2 = EntropyPooling(
mean_views=["AMD >= BAC", "JPM <= prior(JPM) * 0.8"],
cvar_views=["GE == 0.12"],
)
opinion_pooling = OpinionPooling(
estimators=[("opinion_1", opinion_1), ("opinion_2", opinion_2)],
opinion_probabilities=[0.4, 0.5],
)
opinion_pooling.fit(X)
Recognition#
We would like to thank all contributors to our direct dependencies, such as scikit-learn and cvxpy, as well as the contributors of the following resources:
PyPortfolioOpt
Riskfolio-Lib
scikit-portfolio
statsmodels
rsome
Microprediction (Peter Cotton)
Portfolio Optimization Book (Daniel P. Palomar)
quantresearch.org (Marcos López de Prado)
gautier.marti.ai (Gautier Marti)
Citation#
If you use skfolio in a scientific publication, we would appreciate citations:
The library:
@software{skfolio,
title = {skfolio},
author = {Delatte, Hugo and Nicolini, Carlo and Manzi, Matteo},
year = {2024},
doi = {10.5281/zenodo.16148630},
url = {https://doi.org/10.5281/zenodo.16148630}
}
The above uses the concept DOI, which always resolves to the latest release. If you need precise reproducibility, especially for journals or conferences that require it, you can cite the version-specific DOI for the exact release you used. To find it, go to our Zenodo project page, locate the release you wish to reference (e.g. “v0.10.2”), and copy the DOI listed next to that version.
The paper:
@article{nicolini2025skfolio,
title = {skfolio: Portfolio Optimization in Python},
author = {Nicolini, Carlo and Manzi, Matteo and Delatte, Hugo},
journal = {arXiv preprint arXiv:2507.04176},
year = {2025},
eprint = {2507.04176},
archivePrefix = {arXiv},
url = {https://arxiv.org/abs/2507.04176}
}